European XBRL Reporting Entities handbook
From XBRLWiki
(diff) ←Older revision | Current revision | Newer revision→ (diff)
CEN Workshop Agreement
Status: Working Group Working Draft
CEN WS XBRL Experts: Pieter Maillard (Aguilonius), Pablo Navarro (Atos)
Improving transparency in financial and business reporting Standard regulatory roll-out package for better adoption Part 2: XBRL Handbook for Declarers
- Foreword
This document has been prepared by CEN/WS XBRL, the secretariat of which is held by NEN.
CWA XBRL 003 consists of the following parts, under the general title Improving transparency in financial and business reporting Standard regulatory roll-out package for better adoption
- Part 1: XBRL Supervisory Roll-out Guide
- Part 2: XBRL Handbook for Declarers
This CWA is one of a series of related deliverables. The other deliverables are:
CWA XBRL 001 which consists of the following parts, under the general title Improving transparency in financial and business reporting Harmonisation topics:
- Part 1: European data point methodology for supervisory reporting
- Part 2: Guidelines for data point modelling
- Part 3: European XBRL Taxonomy Architecture
- Part 4: European Filing Rules
- Part 5: Mapping between DPM and MDM
CWA XBRL 002 Improving transparency in financial and business reporting Metadata container
- Introduction
The set of recommendations included in this document aim to facilitate the implementation of European National Supervisors to adopt XBRL in any of the reporting frameworks. The following sections will provide guidance on the use, understanding, preparation, and extension of their filings in eXtensible Business Reporting Language (XBRL).
This guidance is in the form of notes in association with the pertaining requirements clause and uses the terms “should”• (recommendation), “may”• (allowance) and “can”• (possibility). Organizations wishing to implement this CWA would be expected to consider all recommendations where the term “should”•is used.
COREP, FINREP (and Solvency II or other future) XBRL taxonomies are offered to European regulators for national implementation. The first releases (2006) of the COREP and FINREP XBRL frameworks have proven that a standardized technical roll-out package is needed to increase the adoption rate and avoid implementation variances, which have a detrimental effect on the overall cross-border effectiveness of using one reporting standard. This roll-out guide tries as well to promote the economies of scale of a better adoption
Scope
This CWA is an introduction to XBRL and serves as a help to preparers of XBRL (reporting entities). The following subjects are addressed in this CWA:
- an introduction to XBRL from a declarer's perspective;
- the basics of XML, the main building block of XBRL, will be explained. Various XML components will be introduced;
- an introduction to XBRL. In this section, XBRL is introduced and various topics are addressed: XBRL taxonomies, extensions, XBRL dimensions, Formulas, the structure of an instance document, the validation of XBRL.
Symbols and abbreviations
For the purposes of this document, the following abbreviations apply.
W3C World Wide Web Consortium
XBRL eXtensible Business Reporting Language
XML eXtensible Markup Language
How to start with XBRL from the declarer's perspective
XBRL stands for eXtensible Business Reporting Language. It is a language for the electronic communication of business information, providing major benefits in the preparation, analysis and communication of business information. It offers cost savings, greater efficiency and improved accuracy and reliability to all those involved in supplying or using business information.
The popularity of XBRL as a communication standard is growing as it is adopted by more and more regulators around the world. Entities reporting information to regulators might initially see XBRL as another reporting burden. However, XBRL provides many benefits for the declarer as well. All organisations can use XBRL to save costs and improve efficiency in handling business and financial information. Because XBRL is extensible and flexible, it can be adapted to a wide variety of different requirements. All participants in the financial information supply chain can benefit, whether they are preparers, transmitters or users of business data.
There are a large number of software tools for creating, manipulating and analysing XBRL, most of which hide all the technical details involved in the expression of XBRL data. To this end, a user doesn't need to understand or even see the XBRL itself. However, a basic understanding of the basic components of XBRL can allow the user to better grasp the potential benefits.
The ambition of this document is to explain the foundations of the XBRL standard. Although these aspects might seem technical at first, all topics will be addressed in a general, comprehensible way.
XML and XBRL: Introduction to the technological building blocks
Introduction
This section aims to present an overview of the basic technologies that underpin XBRL in order to obtain a better understanding of this reporting language. Since XBRL is built upon the XML language, this section focuses on the basics of the XML standard, in particular the XML components which are also used by XBRL.
XML
Introduction
XML, or eXtensible Markup Language, is a W3C standard which enables the representation of structured data in the form of flat text. This simple and flexible text format is both machine readable and human readable. The XML specification, which is a derivative of SGML, uses elements and attributes to structure content. Although originally designed for the publication of information, XML is increasingly important in facilitating a wide range of electronic communications.
In the sections below, we'll elaborate on the following topics:
- XML as a markup language;
- how XML can be used to structure information;
- the main components of an XML document;
- namespaces and prefixes;
- unicode;
- the benefits of XML.
XML as a markup language
Simply put, one can say that XML is a flexible language for expressing structured information in a machine-readable format. Content is “marked up” using "tags" as in the example below. XML is commonly referred to as a "markup" language for this reason. The XML below represents a list of books:
<book>On the Road</book> <book>The Catcher in the Rye</book> <book>The Hobbit</book> <book>The Name of the Rose</book>
The name of each book is delimited by two tags. The first tag contains an identifier enclosed in angle-brackets (<book>), indicating the beginning of a field. The second tag is equal to the first, but also contains a closing bracket (</book>), which indicates the end of a field. As a result, the content of each element of <book> is delimited by the opening and closing tags. With this method, a system that processes this information can easily identify the subject and aim of the provided information
XML structures
The previous example used only a single element: <book>. The XML information model, however, is hierarchical: an element can contain other elements, which in turn can also contain other elements. This is illustrated by the example below.
EXAMPLE XML structure example
<library>
<book>
<title>On the Road</title>
<author>Jack Kerouac</author>
</book>
<book>
<book>
<title>The Catcher in the Rye</title>
<author>J. D. Salinger</author>
</book>
<book>
<book>
<title>The Name of the Rose</title>
<author>Umberto Eco</author>
</book>
<book>
</library>
In the example above, the "library" element contains a set of "book" elements. Each of these "book" elements contains a "title" and an "author" element.
Components of an XML document
The most important components of an XML document are the elements. Elements are defined by their name (e.g. "book", above), their content (the value between the angled brackets, which can be or null – nil) and an indefinite number of attributes. The example below shows an element with two attributes:
EXAMPLE XML element with two attributes
<element attribute1="attr-value1" attribute2="attr-value2">content</element>
An XML document may start with an XML declaration, where the XML version is identified (typically 1.0) as well as the character encoding. This is followed by the first element7. This element is called root element. This will have a number of undetermined "child" elements.
EXAMPLE XML root element
<?xml version="1.0" encoding="UTF-8">
<library>
<!-- other items -->
</library>
The example above shows an XML document which uses version 1.0, has UTF-8 encoding and has "library" as the root element.
The XML specification defines an XML document as a text that is well-formed i.e., it satisfies a list of syntax rules provided in the specification. This list is lengthy, but some key points are:
- Only properly encoded legal Unicode characters are allowed.
- None of the special syntax characters such as "<" and "&" can appear except when performing their markup-delineation roles.
- The begin, end, and empty-element tags that delimit the elements are correctly nested, with none missing and none overlapping.
- The element tags are case-sensitive; the beginning and end tags must match exactly.
- There is a single "root" element that contains all the other elements.
It is also possible to include comments in XML documents. These comments are not processed by applications and allow the inclusion of clarifications in the text document when deemed appropriate. Comments begin with the characters "<!-" and end with the characters "->".
Namespaces
The naming scheme described above is limited, as it can lead to ambiguity between elements which use the same name. Consider the following two examples:
EXAMPLE XML namespaces
<?xml version="1.0" encoding="UTF-8">
<library>
<book author="J.R.R. Tolkien" language="English">The Lord of the Rings</book>
<book author="Molière" language="French">Tartuffe</book>
</library>
<?xml version="1.0" encoding="UTF-8">
<xml-apps>
<tool name="xmlstarlet" language="c"/>
<tool name="trang" language="java"/>
<tool name="xmldiff" language="python"/>
</xml-apps>
The first document contains a representation of a collection of books and the second describes three XML applications. Both make use of the attribute “language”, but the meaning of “language” is different in each case: In the first example the language attribute means the human language of the book; in the second example the language attribute means the programming language of the application.
A human would have little difficulty in distinguishing the use of the same attribute in different contexts. However, for a machine to process the information automatically, ambiguities must be avoided.
XML namespaces are used to provide unique element names and attributes in an XML document. A namespace defines a grouping of concepts. Within a namespace, each concept is identified uniquely by its local name. Globally, each concept is identified uniquely by its local name plus the identifier of its namespace. Local name and namespace identifier together form a ‘Qualified Name’, or QName. The two previous examples could thus be represented as follows:
| Table 1 Table Title Namespace | Local Name | Description |
| Literature | Language | Language, speech |
| Computer Sciences | Language | Programming language |
But how can we ensure that there is no naming conflict at the namespace level? How can we ensure, for example, that there cannot be different interpretations of the namespace "literature"? The unique identification of a namespace is achieved by using a URI (Uniform Resource Identifier).
The following is an example of a URI which could be used a namespace:
EXAMPLE Namespace URI
The fundamental idea behind a namespace is that it incorporates an internet domain as part of its identifier. The use of namespaces allows the definition of unique concepts. This is in an important aspect of the XBRL standard.
Namespaces and prefixes
For readability purposes, XML documents can assign each namespace to a ‘prefix’ (usually a short string). After declaring a prefix for a namespace, all full namespace identifiers can be replaced by the declared prefixes. The association between a prefix and its corresponding namespace is usually set at the root node. The association of a prefix and a namespace is done using a special attribute: xmlns:[prefix]="Namespace". This is illustrated by the example below:
EXAMPLE XML namespace prefix
<?xml version="1.0" encoding="UTF-8">
<bk:book-collection xmlns:bk="http://www.book.org">
<bk:book author="Norman Davies" language="English">Europe: A History</bk:book>
<bk:book author="Homeros" language="Greek">Ilias</bk:book>
<bk:book author="Jonathan Litell" language="French">Les Bienveillantes</bk:book>
</bk:book-collection>
In the above example, ‘xmlns:bk=http://www.book.org”’ binds http://www.book.org to the prefix "bk". Once the namespace is bound, the prefix “bk” can be used in its place, so the element "bk:book" has "book" as its local name and "http://www.book.org" as its namespace.
UNICODE
Unicode is a standard for the representation of text expressed in most of the world's writing systems. Unicode can be used to represent any character in English, Spanish, Greek or any other western language, Chinese, Cyrillic, Hebrew, Arabic, Mongolian, Ethiopian and many others.
Unicode was originally developed by a consortium of companies including Apple, Microsoft, IBM, Xerox, HP and Adobe in order to obtain a universal character set. It is now integrated in almost all modern operating systems as well as technological languages like XML, Java, or the Microsoft .Net Framework. Unicode can be implemented by different character encodings. One of the most commonly used encodings is UTF-8 (which is also compatible with the older ASCII code).
Thanks to the use of Unicode, XML allows the representation of text in any language.
XML Benefits
The previous sections have introduced the main elements of the XML syntax. XML is a markup language which can be used to describe data structures in a machine-readable format.
The benefits of XML are among others:
- language, readable by humans as well as machines;
- It is self-contained. An XML document not only describes the data values, but also its structure and the naming of the fields;
- Its hierarchical structure allows the representation of virtually any data structure in a simple way;
- It is platform-independent, e.g. XML documents can be used on any operating system and with any programming language;
- The use of a strict syntax leads to an efficient processing by tools.
XML is used at the core of all information exchange over the internet.
XML Schema
An XML schema is a collection of XML definitions. These definitions, called schema components, describe the allowed structure and content of an XML document by providing restrictions to the XML syntax itself. The rules defined by an XML schema determine the validity of an XML document using that schema.
XML Schema Components
A schema defines the elements and attributes that make up an XML document. Elements and attributes are defined by stating their name and the possible values they can take (their “type”). Attributes can only be of simple type, while elements can also be of complex type. A complex type allows the specification of an element's valid attributes and specifies complex content: elements that are composed of other elements. An element identified as a simple type cannot contain other elements.
In addition, other auxiliary components exist that, although not directly used in XML documents, can be used in a schema (or in other schemas extending the schema). Auxiliary components include type definitions, groups of elements and groups of attributes.
Predefined types
One of the main features of an XML Schema is that a broad set of types are incorporated by default. These predefined types can in turn be divided into “primitives” and “derivatives”. Derived types are those whose definition is based on another type. Primitive types are the most basic types defined by the specification: these definitions do not depend on other types.
Among the primitive types of the XML Schema are: the string type (a string of characters), the Boolean type (a type with only 2 logical values: true of false), the decimal type (a decimal number with an arbitrary precision), the duration type (represents an extension of time) and the time type (represents a time of the day).
Among the derived types of the XML Schema are: the normalizedString type (a string of characters which cannot contain carriage return, new line or tab), the positiveInteger type (integer number values larger than zero), the negativeInteger type (integer number values smaller than zero).
All of these types are defined in the namespace of the XML Schema. As a result, the types will appear with their corresponding prefix (usually "xs"). For example: "xs:string", "xs:integer", …
Besides these predefined types, XML Schema allows for the creation of many more in order to meet any number of arbitrary requirements.
Extension of simple types
Simple types do not contain XML structures. The possible values for simple types can thus be expressed by a sequence of flat characters. Existing simple types can serve as a basis for the creation of new simple types or can be used in complex types.
Simple types are most commonly extended through the use of a restricting mechanism, via the declaration of properties (facets) to impose limits on the extended base type. For example, if the base type is xs:integer, minimum and maximum values can be defined in order to define a new type.
The properties that can be applied to an extended simple type depend on the base that being extended. For example, the number of digits of a numeric type can be limited, a date can have a maximum value or a regular expression can be applied to a string.
Extension of types: attribute declaration
XML Schema allows the extension of attributes of extended types (simple types do not have any attributes). Conversely; the use of attributes can also be restricted.
Unlike elements, attributes cannot be repeated within the same element. The order in which they are declared in an element is also irrelevant. An XML Schema however, can control whether their use is mandatory, optional or prohibited.
Sometimes it is useful to allow attributes in XML documents that are not defined in the schema. In this case, the component "xs:anyAttribute" is used. This component can be accompanied by a namespace attribute limiting the number of attributes that can be used in the XML document. This is widely used in XBRL, providing flexibility to the schema.
Extension of types: composition of elements
The extension of simple types is not sufficient to express all possible data structures in XML. In order to express nested element structures, we need to compose elements within the schema.
In the following example, the contents of root element "library" may contain the "book" or "audiocd". The elements of type "book" can in turn contain a pair of singles ("title" and "author"), not following a predetermined order. The elements of type "audiocd" contains a list of elements "track-title" and "track-duration" which contains the title information and its duration for each track on the CD:
EXAMPLE XML Schema example
<?xml version="1.0" encoding="UTF-8">
<library>
<book>
<author>Hilary Mantel</author>
<title>Wolf Hall</title>
</book>
<book>
<title>Raghuram Rajan</title>
<author>Fault Lines</author>
</book>
<audiocd album="Kind Of Blue">
<track-title>So What</track-title>
<track-duration>9</track-duration>
<track-title>Freddie Freeloader</track-title><
<track-duration>10</track-duration>
<track-title>Blue In Green</track-title>
<track-duration>5</track-duration><
</audiocd>
</library>
There are three mechanisms in an XML Schema that can be used to define compositional relationships: "sequence", "choice" and "all":
- Sequence: indicates that the content of a type is an ordered list of elements. In the example shown above, "audiocd" contains elements "track-title" and "track-duration"
- Choice: allows the choice of a component from an available list. In the above example, "library" can be expressed as a "choice" of the elements "book" and "audiocd".
- All: allows the creation of an unordered list or set. Unlike "sequence", "all" does not establish an order. In the above example, "book" consists of the elements "title" and "author" without a predetermined order.
This can be schematically represented in the following illustration:
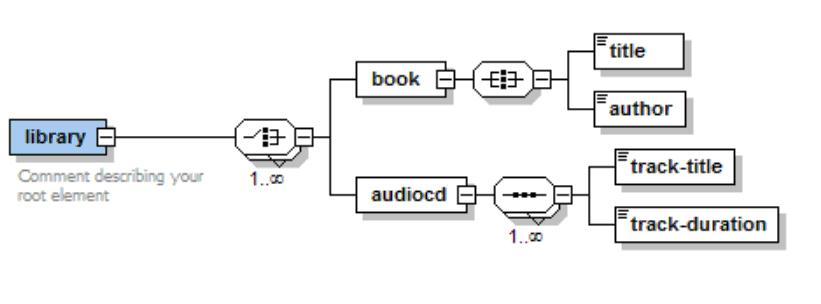
Figure 1 XML Schema example
EXAMPLE EXAMPLE XML Schema example
<?xml version="1.0" encoding="UTF-8">
<xs:schema xmlns:xs="http://www.w3.org/2001/XMLSchema">
<xs:element name="library">
<xs:complexType>
<xs:choice maxOccurs="unbounded">
<xs:element name="book">
<xs:complexType>
<xs:all>
<xs:element name="title">
<xs:element name="author">
</xs:all>
</xs:complexType>
</xs:element>
<xs:element name="audiocd">
<xs:complexType>
<xs:sequence maxOccurs="unbounded">
<xs:element name="track-title">
<xs:element name="track-duration">
</xs:sequence>
</xs:complexType>
</xs:element>
</xs:choice>
</xs:complexType>
</xs:element>
</xs:schema>
As explained in the previous sections, the prefix "xs:" points to the namespace "http://www.w3.org/2001/XMLSchema". The number of repetitions or cardinality of the elements can be controlled by the attributes "minOccurs" and "maxOccurs". The combination of these attributes with different elements can result in more complex schemas.
ID and IDREF attribute types
A number of specific attribute types, which exist in XML Schema, are particularly significant in XBRL. These attribute types are ID and IDREF.
The value assigned to an ID type attribute can't be repeated within the same XML document. As a result, an ID type attribute uniquely identifies each element within the same document.
In the example below, the ISBN attribute has been defined in the corresponding XML schema as an ID type attribute:
EXAMPLE ID type attribute
<?xml version="1.0" encoding="UTF-8">
<library>
<book ISBN="ISBN-0-262-56099-2">It's not about the Bike</book>
<book ISBN="ISBN-0-262-56099-2">The Pillars of the Earth</book>
<book ISBN="ISBN-0-569-00108-8">A History of the World in 100 Objects</book>
</library>
According to XML Schema rules, this example is invalid, because there are two books with the same ID.
The attribute type IDREF is a reference to another ID. In other words, an attribute of IDREF type must contain the value of an ID which already exists in the document. This is illustrated in the example below, where a new attribute called "sequel-of" is an IDREF:
EXAMPLE XML Schema example
<?xml version="1.0" encoding="UTF-8">
<library>
<book ISBN="ISBN-0-262-56099-2">The Fellowshiop of the Ring</book>
<book ISBN="ISBN-0-311-57018-9" sequel-of=" ISBN-0-262-56099-2">The Two Towers</book>
<book ISBN="ISBN-0-569-00108-8" sequel-of=" ISBN-0-311-57018-9">The Return of the King</book>
</library>
Groups of attributes and elements
In some cases, a number of attributes are used repeatedly in elements of a schema. In that case, a group of attributes can be used: it is the group that is referenced in the element declaration.
Similarly, elements can also be declared as a group of content types. For example, the "choice" type refers to a group of elements, which enable the selection of any element defined in that group.
Importing and including schemas
XML schemas can import or include other schemas. Doing this allows the use of components (elements, types, attributes and groups) defined in other schemas. When the imported schema belongs to a different namespace “import” is used ("xs:import") . If the namespace is the same, “include” is used ("xs:include").
The use of import and include means that XML schemas can be easily extended. This simplifies the definition of a new schema, since existing definitions can be imported. This is used extensively in the XBRL standard.
XML Schema benefits
The use of XML Schema simplifies information processing. Some of the benefits of XML Schema:
- A Schema document defines a common structure. As a result, automated processing of this document is streamlined.
- Adequacy checks can be performed using market tools (validators), instead of custom development. This improves quality as well as reducing the development time of new applications
- Reuse of market software. Besides validators, a large number of existing tools also make use of XML Schemas. For example: exhibit generators, database extraction & storage utilities, publishers, ...
- Development can be based on the data types associated with components, instead of the components themselves. This makes development more flexible and makes it more likely that code will be reused.
- Reuse of global definitions. Via the use of namespaces and the import of existing schemas, concepts defined by different organisations can be reused.
XLink
XML Linking Language or XLink is a standard defined by the W3C that creates and describes cross-references between resources or fragments of XML documents. For example, XLink allows the creation of links which are similar to hyperlinks.
Technological components used by XML and by XBRL
This section describes some technologies which, while not part of the current version of the XBRL standard, allow generic XML document processing, and therefore can also be used for XBRL processing.
XPath
XPath is a language that enables the selection of fragments in an XML document. It also allows basic manipulation of strings, numbers and logical expressions. XPath uses a compact syntax, resembling in some ways the syntax used by old operating systems to identify a file or a set of files (but replaces directories with XML tree nodes)
| EXAMPLE XPath examples Xpath Expression | Result |
| /library/author/book | selects all books of the library |
| /library/author[@name="JRR Tolkien"]/book | selects all books authored by JRR Tolkien |
| /count(library/author[@name="JRR Tolkien"]/book) | returns the number of books authored by JRR Tolkien |
| /library/author[@name="JRR Tolkien"]/book [last()] | selects the last book authored by JRR Tolkien |
| //@ISBN | selects the ISBN attribute value of any XML tree node |
XPath is perhaps more important for its use as part of other standards like XSLT or XQuery, than use on its own.
XSLT
XSLT (or Extensible Stylesheet Language Transformations) is a language for transforming XML documents. It uses a scheme of pattern matching: the user defines a set of patterns (defined in XPath) and results. When an XSLT processor locates a fragment that fits one of these patterns, the corresponding result is substituted in the output document. XSLT incorporates additional features such as control structures and the definition of functions or lookup tables. These additional features make XSLT a powerful language.
The illustration below shows a functional diagram of an XSLT processor:
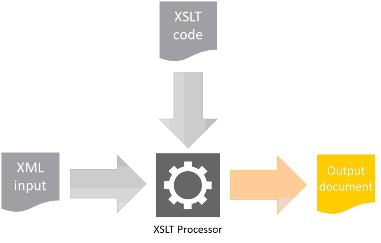
Figure 2 Functional diagram of an XSLT processor
XQuery
The previous sections give the reader a flavour of how XML can be used to represent structured information. There are databases that use XML as an alternative (or complement) to conventional technologies such as relational databases. The need to query XML data thus arises. This is addressed with XQuery, a functional programming language designed to query collected XML data.
XBRL: Extensible Business Reporting Language
The aim of this section is to give an explanation of the main features of XBRL as a language for representing business information. The content is intended to be presented a conceptual level (and thus does not go into too much technical detail).
How to structure reporting data?
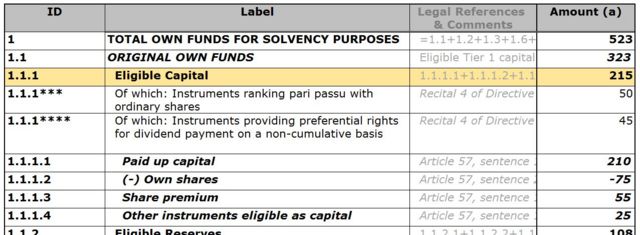
Before starting to explain XBRL, the advantage of structuring reported data is shown with an example. Reported financial data tend to be represented in a table. For example, the COREP Capital Adequacy table:
EXAMPLE Eligible Capital concept
<p-ca:EligibleCapital>215</p-ca:EligibleCapital>
Although this tag provides some semantic information, extra information is missing. For numeric facts, the unit is defined by the content of a unit element, referenced by the unitRef attribute of facts, for example, to define a monetary value as being expressed in euros:
EXAMPLE Eligible Capital concept, with unit:
<p-ca:EligibleCapital unitRef=”EUR”>215</p-ca:EligibleCapital>
The context element, referenced by the contextRef attribute of facts, is used to convey: the reporting entity, the reporting period or reference date and, optionally, dimensional characteristics:
EXAMPLE Eligible Capital concept, with unit and context
<p-ca:EligibleCapital unitRef=”EUR” contextRef=”2012-12-31”>215</p-ca:EligibleCapital>
The above example shows, in a nutshell, how XBRL allows the structuring of reporting data
XBRL Introduction
XBRL, or eXtensible Business Reporting Language, is a communication language developed for the standardised exchange of business and financial data.
XBRL normalises the format of the data (via the use of XML techniques) and the validation of data (via XBRL taxonomies)
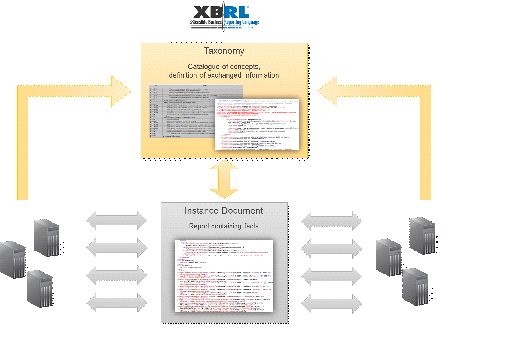
Figure 4 Interaction between an XBRL taxonomy & an XBRL instance document
- standard validation rules (mathematical and logical rules);
- the use of label linkbases (which allows multi-lingual taxonomies);
- mechanisms for defining a human-readable rendering.
- XBRL Taxonomies;
- the extensibility of XBRL;
- XBRL Dimensions;
- XBRL Formulas;
- XBRL instance documents;
- the validation of XBRL instance documents.
XBRL Taxonomies
An XBRL Taxonomy defines the concepts of a certain domain and the relationships between them. XBRL taxonomies are a collection of taxonomy schemas and linkbases.
Schemas
Based on XML Schema, a taxonomy schema defines concepts and their basic properties.
Each concept is represented by an element in a schema. As a result, each concept will have a qualified name (i.e. namespace plus local name). As previously explained, this will allow unique identification of the specific concept.
All basic properties of a concept are expressed as element attributes. The values of these properties determine how the concept will be used to represent concept values, known as “facts” in an XBRL report. The most common properties are:
- Data type: the type of value (monetary, value, percentage, text ...) that can be assigned to the concept. Predefined XBRL types can be used, or new ones can be defined using XML Schema.
- Period type: generally, two period types are used in XBRL:
- Instant: used for expressing facts which refer to a certain moment in time (e.g. an amount on a balance sheet)
- Duration: used for expressing facts which refer to a time interval (e.g. revenue for a certain period)
In addition to these predefined properties, the flexibility of XBRL allows the creation of taxonomy-specific properties.
Linkbases
Linkbases are used to define relationships between elements and relationships between resources. A resource can be, for example, the label of a concept in specific language or a reference to a paragraph of a legal document.
These relationships are defined using the XLink standard. Each link has a specific type. XBRL defines a set of predefined types that are grouped into linkbases. Linkbases in common use are:
- Label linkbase: Used to assign labels to concepts defined in a schema. Multiple labels for different purposes (e.g. “Documentation”, “Period Start”, “Short Label”…) can be assigned to each concept. Each label may be expressed in different languages.
- Reference linkbase: Used to link concepts to references to specific regulations. This could be the whole text of the regulation, and/or only a reference to the full text.
- Presentation linkbase: Used to establish hierarchical relationships between the concepts defined in a schema. The presentation linkbase is generally used as a graphical guide for filing XBRL reports, since concepts can be displayed in a tree structure which matches the presentation relationships defined. The Presentation linkbase allows different presentations of the business concepts.
- Definition linkbase: Originally planned for defining simple validation relationships between concepts, such as dependencies (e.g. if concept A is reported in a document, concept B must be reported as well), the definition linkbase is more commonly used to define dimensional relationships according to the Dimensions 1.0 specification, which will be discussed in a later section.
- Calculation linkbase: Used to define simple aggregation relationships between different elements. For example: concept A may be calculated as the sum of A1, A2, A3 ... These aggregations can be modified with specific weights in order to obtain more complex arithmetic operations.
Extensibility
XBRL is extensible by design. The original authors of XBRL were aware of the complexity and diversity of reporting all over the world. As result, XBRL was designed to be a flexible language in order to suit as many use-cases as possible. In addition to the extensible nature of the language itself, taxonomies (schemas) can be extended with additional concepts and new relationships.
The idea behind extending a taxonomy is to build upon an existing taxonomy, and the concepts and relationships it defines, to incorporate additional information. For example, a taxonomy which defines concepts relating to an international standard can be extended in order to better define the information required by local regulators.
Taxonomy extensions can be created by importing one or multiple existing taxonomies (using XML Schema’s ‘import’ as described before, or using references from linkbases). In addition to the concepts and relationships defined in the imported taxonomies, the resulting new taxonomy may also include new concepts and relationships between (new or existing) concepts
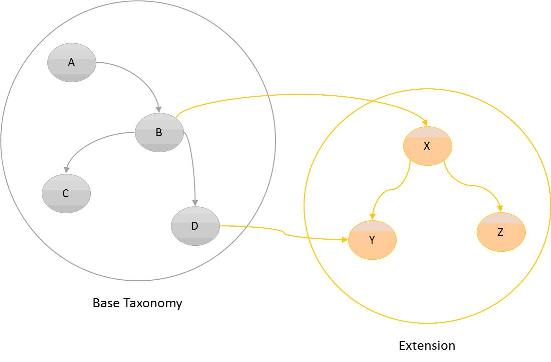
Figure 5 XBRL Taxonomy extension
Dimensions
The multidimensional data model
Multidimensional data models are known for their use in the analysis of business information. Such analytical processing, known as ‘OLAP’ (Online Analytical Processing), has been widely used across the software industry for a number of years.
The basic elements of this model are: metrics, dimensions, domains and hypercubes. Metrics represent primary business concepts (line items, or ‘primary items’). Dimensions represent ways to break down the data, or to express characteristics (for example: “before mitigation” or “after mitigation”). Examples of dimensions include: Time, product line, clients, geography. The set of possible values within a dimension is called a domain.
The reported values within a dimensional model (also known as facts) will always relate to a specific set of dimensional values. For example, revenue (metric) is 100.000€ in Croatia (“Country of sale” dimension), for snails (“Product” dimension), before tax (“Fiscal characteristics” dimension).
The elements that make up the domain of dimension are often ordered hierarchically. For example, the domain for the customer dimension could be divided into large companies, medium-sized companies and small companies.
The same domain can be used in different dimensions. For example, the representation of a bank transfer can include a dimension indicating the country of origin as well as a dimension indicating the destination country. The values that these two dimensions can take are identical: the country domain.
The set of possible combinations of dimension values for a given metric is called a hypercube. The name hypercube comes from the common representation of a multidimensional model:
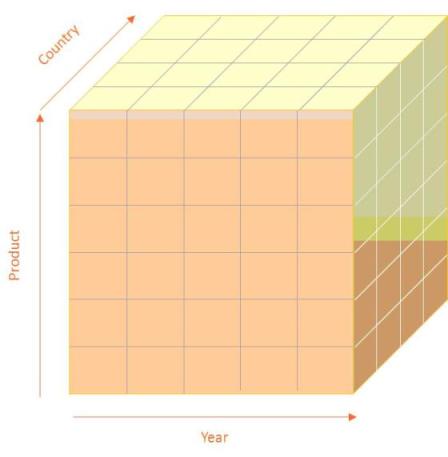
Figure 6 Graphical representation of a 3-dimensional hypercube
XBRL dimensions
The XBRL Dimensions specification has been at the official recommendation level as a standard since September 2006. This extension to the XBRL standard allows the definition of valid combinations of dimensions to further contextualise a reported primary item value, and defines elements of these domains. This information is expressed in the taxonomy via relationships in the definition linkbase.
There are two types of XBRL dimension:
- Explicit dimensions are dimensions whose domain is defined by ‘domain member’ elements are listed explicitly (and perhaps arranged into a hierarchy, as with the large, medium and small company example).
- Typed dimensions are dimensions whose elements are not predefined. These dimensions are used when it is not possible to define explicit values, but a possible range, instead. For example, the 10-digit ISBN code of a book could be defined as a typed dimension with a domain restricted to a string matching the following pattern: ISBN\s(?=[-0-9xX ]{13}$)(?:[0-9]+[- ]){3}[0-9]*[xX0-9]
One characteristic of the dimensions specification is that it allows taxonomies to define invalid dimension combinations. For example, a taxonomy has two dimensions: fruit & colour. The taxonomy can thus indicate that some combinations of dimension values are not allowed (for example: "banana" & "red").
The dimension specification is a major contribution to the XBRL standard, as it allows an intuitive representation of business information.
Formulas
The XBRL Formula specification has been at the official recommendation level as a standard since June 2009. The main goal of the XBRL Formula specification is to provide validation capabilities not present in the base specification (XBRL 2.1).
The Formula Specification supports the creation of expressions (using XPath) that can be applied to XBRL instances. XBRL Formulas can be used to validate the information within an instance document.
XBRL Formulas can also be used to calculate new XBRL facts in a new instance (output instance). This output instance can be used to represent many variations on the data derived from an instance, such as transformations or determination of ratios.
XBRL Reporting: Instance document structure
After explaining all the various components of XBRL, which explain how XBRL works, it might be interesting to explain how XBRL is reported. The illustrated example has already indicated how reported data is represented in the XBRL format. In this section, the structure of an XBRL document, also called an instance document, will be explained.
XBRL instance documents do not have an elaborate predefined tree structure as may be the case in some XML schemas. All elements of an instance document reside directly within the major <xbrl> root node. Nevertheless, some components can always be found in an XBRL instance.
These components will be explained into more detail with the use of an example instance document.
XBRL root node, namespaces and schemaRef
Every XBRL instance document starts with the XML declaration, followed by the <xbrl> root node. Within the root node, namespaces used in the instance document can be declared. In the example below
namespaces have been declared. All subsequent elements in the instance document are directly below the <xbrl> root node.
EXAMPLE XBRL root node, with namespaces an schemaRef
<?xml version="1.0" encoding="UTF-8">
<xbrl>
xmlns="http://www.xbrl.org/2003/instance"
xmlns:d-Regions-be="http://www.c-ebs.org/eu/fr/esrs/finrep/d-Regions-be/2008-01-01"
xmlns:d-sc-be="http://www.c-ebs.org/eu/fr/esrs/corep/2006-07-01/d-sc-be-2006-07-01"
xmlns:ifrs-gp="http://xbrl.iasb.org/int/fr/ifrs/gp/2006-08-15"
xmlns:iso4217="http://www.xbrl.org/2003/iso4217"
xmlns:link="http://www.xbrl.org/2003/linkbase"
xmlns:p-FINREP="http://www.c-ebs.org/eu/fr/esrs/finrep/p-FINREP/2008-01-01"
xmlns:xbrldi="http://xbrl.org/2006/xbrldi"
xmlns:xbrli="http://www.xbrl.org/2003/instance"
xmlns:xlink="http://www.w3.org/1999/xlink"
xmlns:xsi="http://www.w3.org/2001/XMLSchema-instance">
<link:schemaRef xlink:type="simple"
xlink:href="http://www.c-ebs.org/eu/fr/esrs/finrep/t-FINREP-be/BalanceSheet/2008-01-01/t-FINREP-be-2008-01-01-T01-BalanceSheet.xsd"/>
...
</xbrl>
The first element shown in the above example is the link:schemaRef element, which indicates the location of the entry point for the XBRL taxonomy against which this instance document is expected to be valid. In the example above, the relevant taxonomy entry point is "t-FINREP-be-2008-01-01-T01-BalanceSheet.xsd" (corresponding to the Balance Sheet table of the Belgian Finrep report). For this instance document to be XBRL valid, it will have to valid against the definitions in t-FINREP-be-2008-01-01-T01-BalanceSheet.xsd.
The use of UTF-8 encoding is also recommended as best practice in [CWA1], since it is recognised as the preferred and most used type of encoding in HTML.
Contexts and units
After these first general elements, the contexts and units are defined.
Contexts give additional information to reported data, like:
- Related timing of the reported data. This can be a period (duration) or a moment in time (instant);
- Identification of the reporting entity;
- Dimensional information. If the reported data is linked to a combination of a primary concept and dimensional values, the dimensional definition will need to be included in the context.
To fully contextualise a numeric fact in an instance, it must be associated with a unit. Units indicate in what measure the reported numeric data is expressed. This could, for example, be a currency (as below).. Other examples of unit are ‘percentage’, ‘pure’ (no unit), ‘earnings per share’.
EXAMPLE XBRL instance document, with unit & context definitions
...
<context id="I-2007-12-Belgium">
<entity>
<identifier scheme="http://www.swift.com">TESTST04</identifier>
</entity>
<period>
<instant>2007-12-31</instant>
</period>
<scenario>
<xbrldi:explicitMember dimension="d-Regions-be:ByRegionsDimension">d-Regions-be:Belgium</xbrldi:explicitMember>
<xbrldi:explicitMember dimension="d-sc-be:ScopeDimension">d-sc-be:Consolidated</xbrldi:explicitMember>
</scenario>
</context>
<context id="I-2007-12-OtherEMU">
<entity>
<identifier scheme="http://www.swift.com">TESTST04</identifier>
</entity>
<period>
<instant>2007-12-31</instant>
</period>
<scenario>
<xbrldi:explicitMember dimension="d-Regions-be:ByRegionsDimension">d-Regions-be:OtherEMU</xbrldi:explicitMember>
<xbrldi:explicitMember dimension="d-sc-be:ScopeDimension">d-sc-be:Consolidated</xbrldi:explicitMember>
</scenario>
</context>
<context id="I-2007-12-RestOfTheWorld">
<entity>
<identifier scheme="http://www.swift.com">TESTST04</identifier>
</entity>
<period>
<instant>2007-12-31</instant>
</period>
<scenario>
<xbrldi:explicitMember dimension="d-Regions-be:ByRegionsDimension">d-Regions-be:RestOfTheWorld</xbrldi:explicitMember>
<xbrldi:explicitMember dimension="d-sc-be:ScopeDimension">d-sc-be:Consolidated</xbrldi:explicitMember>
</scenario>
</context>
<unit id="U-Monetary">
<measure>iso4217:EUR</measure>
</unit>
...
In the example above, three contexts are defined, with the following ID's:
- I-2007-12-Belgium
- I-2007-12-OtherEMU
- I-2007-12-RestOfTheWorld
All three contain dimensional information regarding two XBRL dimensions: ScopeDimension and ByRegionsDimension. One unit is defined (U-Monetary), indicating the use of the EURO currency.
Facts and primary concepts
The reported data in an XBRL instance document are known as ‘facts’. A fact is reported by referring to its primary concept (defined by the taxonomy) and references to its contextual information defined by a context element, a unit element and a number of other attributes depending on the data type of the concept being reported. EXAMPLE: XBRL instance document, with facts and primary concepts
...
<ifrs-gp:CashAndBalancesWithCentralBanks contextRef="I-2007-12-Belgium" decimals="2" unitRef="U-Monetary">2970321000</ifrs-gp:CashAndBalancesWithCentralBanks>
<ifrs-gp:CashAndBalancesWithCentralBanks contextRef="I-2007-12-OtherEMU" decimals="2" unitRef="U-Monetary">709174000</ifrs-gp:CashAndBalancesWithCentralBanks>
<ifrs-gp:CashAndBalancesWithCentralBanks contextRef="I-2007-12-RestOfTheWorld" decimals="2" unitRef="U-Monetary">753252607</ifrs-gp:CashAndBalancesWithCentralBanks>
<ifrs-gp:FinancialAssetsHeldForTradingTotal contextRef="I-2007-12-Belgium" decimals="2" unitRef="U-Monetary">4601911527</ifrs-gp:FinancialAssetsHeldForTradingTotal>
<ifrs-gp:FinancialAssetsHeldForTradingTotal contextRef="I-2007-12-OtherEMU" decimals="2" unitRef="U-Monetary">29760434449</ifrs-gp:FinancialAssetsHeldForTradingTotal>
<ifrs-gp:FinancialAssetsHeldForTradingTotal contextRef="I-2007-12-RestOfTheWorld" decimals="2" unitRef="U-Monetary">23396601036</ifrs-gp:FinancialAssetsHeldForTradingTotal>
<ifrs-gp:FinancialAssetsDesignatedAsFairValueThroughProfitOrLossTotal contextRef="I-2007-12-Belgium" decimals="2" unitRef="U-Monetary">1364964840</ifrs-gp:FinancialAssetsDesignatedAsFairValueThroughProfitOrLossTotal>
<ifrs-gp:FinancialAssetsDesignatedAsFairValueThroughProfitOrLossTotal contextRef="I-2007-12-OtherEMU" decimals="2" unitRef="U-Monetary">231126000</ifrs-gp:FinancialAssetsDesignatedAsFairValueThroughProfitOrLossTotal>
<ifrs-gp:FinancialAssetsDesignatedAsFairValueThroughProfitOrLossTotal contextRef="I-2007-12-RestOfTheWorld" decimals="2" unitRef="U-Monetary">1594727199</ifrs-gp:FinancialAssetsDesignatedAsFairValueThroughProfitOrLossTotal>
<ifrs-gp:AvailableForSaleFinancialAssetsTotal contextRef="I-2007-12-Belgium" decimals="2" unitRef="U-Monetary">17399874637</ifrs-gp:AvailableForSaleFinancialAssetsTotal>
<ifrs-gp:AvailableForSaleFinancialAssetsTotal contextRef="I-2007-12-OtherEMU" decimals="2" unitRef="U-Monetary">29728469000</ifrs-gp:AvailableForSaleFinancialAssetsTotal>
<ifrs-gp:AvailableForSaleFinancialAssetsTotal contextRef="I-2007-12-RestOfTheWorld" decimals="2" unitRef="U-Monetary">5565266331</ifrs-gp:AvailableForSaleFinancialAssetsTotal>
<ifrs-gp:LoansAndReceivablesTotal contextRef="I-2007-12-Belgium" decimals="2" unitRef="U-Monetary">81536712304</ifrs-gp:LoansAndReceivablesTotal>
<ifrs-gp:LoansAndReceivablesTotal contextRef="I-2007-12-OtherEMU" decimals="2" unitRef="U-Monetary">54521384945</ifrs-gp:LoansAndReceivablesTotal>
<ifrs-gp:LoansAndReceivablesTotal contextRef="I-2007-12-RestOfTheWorld" decimals="2" unitRef="U-Monetary">35605182080</ifrs-gp:LoansAndReceivablesTotal>
<ifrs-gp:HeldToMaturityInvestmentsTotal contextRef="I-2007-12-Belgium" decimals="2" unitRef="U-Monetary">345118000</ifrs-gp:HeldToMaturityInvestmentsTotal>
<ifrs-gp:HeldToMaturityInvestmentsTotal contextRef="I-2007-12-OtherEMU" decimals="2" unitRef="U-Monetary">2503013000</ifrs-gp:HeldToMaturityInvestmentsTotal>
<ifrs-gp:HeldToMaturityInvestmentsTotal contextRef="I-2007-12-RestOfTheWorld" decimals="2" unitRef="U-Monetary">162337689</ifrs-gp:HeldToMaturityInvestmentsTotal>
<ifrs-gp:HedgingAssetsTotal contextRef="I-2007-12-Belgium" decimals="2" unitRef="U-Monetary">5977474</ifrs-gp:HedgingAssetsTotal>
<ifrs-gp:HedgingAssetsTotal contextRef="I-2007-12-OtherEMU" decimals="2" unitRef="U-Monetary">145571284</ifrs-gp:HedgingAssetsTotal>
<ifrs-gp:HedgingAssetsTotal contextRef="I-2007-12-RestOfTheWorld" decimals="2" unitRef="U-Monetary">178358452</ifrs-gp:HedgingAssetsTotal>
</xbrl>
This example illustrates several of the ideas presented earlier in this document: Namespaces prefixes are used, along with element names to referencethe element definitions of the primary concepts. Contexts and units references are used to give contextual information to the reported numbers.
The instance document ends with the closing tag of the main <xbrl> root node.
Validation of XBRL reports
One of the fundamental processes required in the handling of XBRL data is the validation of instance documents. The goal of the validation process is the ensure consistency of the reported information according to the different rules imposed by the XBRL standard and by the referenced XBRL taxonomy.
The validation process involves the following steps:
- XML validation: an XBRL document must be a well-formed XML document
- XML Schema validation: an XBRL document must be valid according the schemas used in the taxonomy (its structure, data types, etc.)
- XBRL validation structure. Some rules which are not covered by the taxonomy's schema validation are defined by the XBRL specification. For example, a numeric concept must be accompanied by a unit.
- Validation rules: an XBRL taxonomy can contain certain restrictions defined within the taxonomy linkbases (such as the calculation linkbase).
- Dimensional validation: reported information needs to be valid against the dimensional constraints imposed by the taxonomy. A dimension may not take values that are not specified in its domain, o a metric may not be reported for an invalid combination of dimensions
- Formula validation: if the taxonomy contains XBRL formulas, the reported information may be assessed according to the formulas defined in the taxonomy
All validation steps are generally executed by specific XBRL software
Annex A (informative) Further Readings
Standards & Specifications
- XBRL International - overview of XBRL Specifications: http://www.xbrl.org/SpecRecommendations/
- The XBRL 2.1 Specification: http://www.xbrl.org/Specification/XBRL-2.1/REC-2003-12-31/XBRL-2.1-REC-2003-12-31+corrected-errata-2013-02-20.html
- The XBRL Dimensions Specification: http://www.xbrl.org/specification/dimensions/rec-2012-01-25/dimensions-rec-2006-09-18+corrected-errata-2012-01-25-clean.html
- The XBRL Formula Specification: http://www.xbrl.org/specification/formula/rec-2011-10-24/index-2011-10-24.htm
- W3C overview of XML technologies: http://www.w3.org/standards/xml/
- W3C Recommendation of XML: http://www.w3.org/TR/REC-xml/
- W3C Recommendation of XML Namespaces: http://www.w3.org/TR/REC-xml-names/
- W3C Recommendation of XML Schema: http://www.w3.org/TR/xmlschema-1/
General info
- http://www.xbrl.org/GettingStarted
- http://www.xbrl.org/how-xbrl-works-1
- http://www.eurofiling.info/documents/documents_project.shtml
- http://www.wikixbrl.info/index.php?title=Main_Page
Bibliography
[1] The Extensible Markup Language (XML), see http://www.w3.org/XML/
[2] The XML standard, see http://www.w3.org/TR/2008/REC-xml-20081126/
[3] The eXtensible Business Reporting Language (XBRL), see http://www.xbrl.org/TheStandard
[4] Extensible Business Reporting Language (XBRL) 2.1, available at : http://www.xbrl.org/specification/xbrl-recommendation-2003-12-31+corrected-errata-2012-01-25.htm
[5] XBRL Dimensions 1.0, available at: http://www.xbrl.org/specification/dimensions/rec-2012-01-25/dimensions-rec-2006-09-18+corrected-errata-2012-01-25-clean.html
[6] XBRL Registry specification 1.0, available at: http://www.xbrl.org/Specification/registry/REC-2009-06-22/registry-REC-2009-06-22.html
[7] XBRL Formula specification 1.0, available at: http://www.xbrl.org/Specification/formula/REC-2009-06-22/overview/Formula-Overview-REC-2009-06-22.rtf
[8] New Technical and Normative Challenges for XBRL: Multidimensional in the COREP Taxonomy. Boixo, I.; Flores, F.; July 18th, 2005. The International Journal of Digital Accounting Research, Vol. 5, N. 9, 2005, pages 79-104. ISSN:1577-8517
[9] XBRL for Interactive Data: Engineering the Information Value Chain Debreceny, Roger; Felden, Carsten; Ochocki Bartosz; Piechocki, Maciej; Piechocki, Michal. 2009. Springer, Dordrecht Heidelberg London New York. ISBN 978-3-642-01436-9
[10] XBRL and the Multidimensional Data Model. Santos, I.; Castro, E.; May 6th-9th. 2011. In Proceedings of the 7th International Conference on Web Information Systems and Technologies, WEBIST 2011, pages 161-164, Noordwijkerhout, The Netherlands.
[11] XBRL Interoperability through a Multidimensional Data Model. Santos, I.; Castro, E.; December 8th-10th, 2011. IADIS Internacional Conference on Internet Technologies & Society (ITS 2011). Shanghai, China,
[12] Data Model and Matrix Schemas. Heinze, K.; November 16th-20th 2009. XI European Banking Supervisors XBRL Workshop, November 16th-20th 2009, Vienna, Austria