CEBS Data Model
From XBRLWiki
| Revision as of 06:46, 3 December 2009 (edit) Katrin (Talk | contribs) (→[http://groups.google.com/group/eurofiling/web/FINREP%20Matrix%20schema%202.0.zip FINREP Matrix Schema 2.0]) ← Previous diff |
Current revision (10:57, 14 August 2011) (edit) Iboixo (Talk | contribs) |
||
| Line 1: | Line 1: | ||
| - | [[Image:Corep_finrep_logo.gif]] | + | [[Image:Eurofiling-pp.jpg]] |
| <br/><br/> | <br/><br/> | ||
| Contribution dated 2009-11-03 | Contribution dated 2009-11-03 | ||
| Line 7: | Line 7: | ||
| ===Abstract=== | ===Abstract=== | ||
| + | |||
| + | This document should help users of the CEBS taxonomie (COREP and FINREP) to understand the '''Matrix Schemas''' published on | ||
| + | [http://www.eurfiling.info www.eurfiling.info] web site. In the following the basic aspects of the mulitdimensional data models are explained. | ||
| + | |||
| + | ===Multidimensional terminology=== | ||
| + | |||
| + | ====Description==== | ||
| + | |||
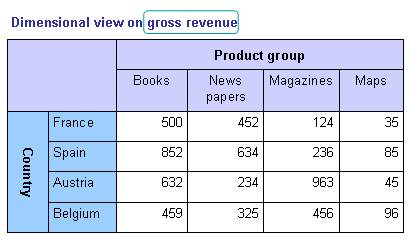
| + | Most of the data presented in tables can be divided in different categories or rather breakdowns. | ||
| + | In the table below the gross revenue is broken down by product group and country. The | ||
| + | information contained is far more detailed as showing only the aggregated sum of gross revenue | ||
| + | and allows therefore a more comprehensive analysis. Multidimensionality is widely used for | ||
| + | cost accounting and the corresponding supervision. | ||
| + | |||
| + | [[Image:Multidimensional_table.gif]] | ||
| + | |||
| + | The table shows a two dimensional view on the data but in fact three dimensions are included. | ||
| + | |||
| + | ====Measures==== | ||
| + | |||
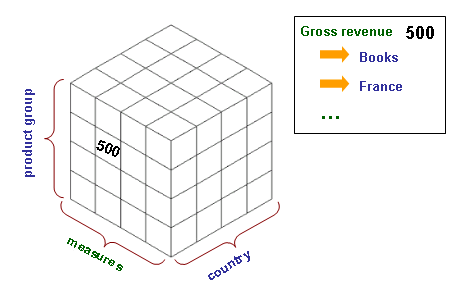
| + | The data that is analysed often in aggregations are called maeasures because they are (mostly) numeric values and measureable. | ||
| + | Having only gross revenue and a value is not enough to interpret the data so they are analysed by using "by" conditions. | ||
| + | Those "by" conditions are reflected in the example above "by" product group and "by" country. | ||
| + | |||
| + | Multidimensional data is often shown as three dimensional cube. The restriction on three dimensions is based on the limitations of the graphical representation. | ||
| + | |||
| + | [[Image:Measures.gif]] | ||
| + | |||
| + | A cell in the cube corresponds to a cell in the table. | ||
| + | |||
| + | ====Dimensions==== | ||
| + | |||
| + | "By" conditions are called dimensions. Dimensions are views for which data should be stored and they can vary depending on the underlying framework. Some dimensions can be seen as general like time or measure unit. | ||
| + | |||
| + | In the example above the country represents a list of possible countries but other dimensions also representing countries could be "country of origin" or "buying country". | ||
| + | |||
| + | ====Domain==== | ||
| + | |||
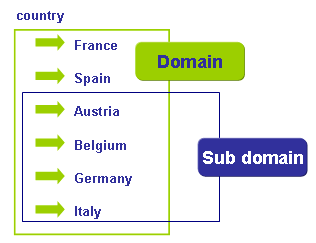
| + | A domain is a set of items having a specific coherence. This domain can be assigned to a dimension. | ||
| + | A sub domain is a subset of items of a domain. A sub domain can also be assigned to a dimension, ie. European countries. | ||
| + | |||
| + | [[Image:Domain.gif]] | ||
| + | |||
| + | In the CEBS framework domains consists of all possible breakdown items like exposure classes or counterparties. If one table does not include all the possible items and using only a shortened list, a sub domain is created. | ||
| + | |||
| + | |||
| + | ====Domain member==== | ||
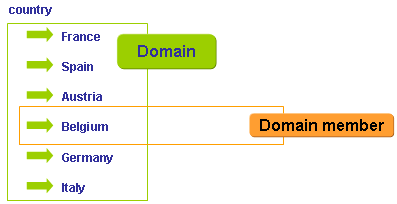
| + | |||
| + | One item in the data set representing a domain is called domain member. In a CEBS taxonomy they are built up in a domain-member-ship. | ||
| + | |||
| + | [[Image:Domain_member.gif]] | ||
| + | |||
| + | Each combination of a measure with the according dimension - domain member combinations identifies a data set uniquely. | ||
| + | |||
| + | |||
| + | ====Hypercube==== | ||
| + | |||
| + | A hypercube defines the cartesian product of the combinations of measures and dimensions. | ||
| + | Hypercubes can be assigned to measures. A grahical representation of a hypercube in an XBRL | ||
| + | taxonomy is shown below. The dimension members are attached to a domain. The domains are | ||
| + | attached to a dimension and the dimensions are assigned to a hypercube. | ||
| + | |||
| + | [[Image:Hypercube.gif]] | ||
| + | |||
| + | Depending on the position of the measure in the hierarchy (domain-member-ship) a hypercube can be defined for cells, group of cells or a complete cube (table). | ||
| + | |||
| + | [[Image:Hypercubes.gif]] | ||
| + | |||
| + | |||
| + | ====Section==== | ||
| + | |||
| + | In this case the example table has been extended by an additional breakdown of book category. | ||
| + | |||
| + | [[Image:Section_table.gif]] | ||
| + | |||
| + | The table can be devided in different parts which are characterised by different number of breakdowns. Both tables refer to the same measure but the first one consists of two dimensions and the second one of three. | ||
| + | A Cartesian product is the product of two sets, so the product set contains all possible combinations of one element from each set. The idea can be extended to products of any number of sets. The product set based on two finite sets can be represented by a table. Each cell of this table is a combination of one element of the set row and one element of the set column. | ||
| + | |||
| + | [[Image:Sections_one.gif]] | ||
| + | |||
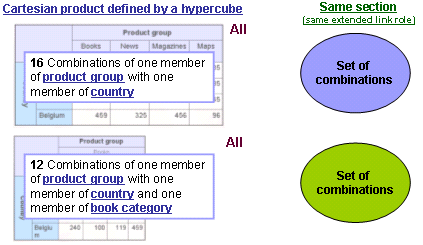
| + | In the example above the Cartesian product of section one consists of 16 Combinations of one member of <span style="color:#5555BB;font-weight:bold;">product group</span> with one member of <span style="color:#5555BB;font-weight:bold;">country</span>. Section two contains 12 Combinations of one member of <span style="color:#5555BB;font-weight:bold;">product group</span> with one member of <span style="color:#5555BB;font-weight:bold;">country</span> and one member of <span style="color:#5555BB;font-weight:bold;">book category</span>. | ||
| + | |||
| + | In XBRL Cartesian products are represented by hypercubes defined in extended link roles within the definition linkbase. Hypercubes that contain combinations that are allowed to be reported, are defined as all hypercubes. With reference to the example above both hypercubes represent allowed combinations. In the picture below both hypercubes are defined in the same extended link role. | ||
| + | |||
| + | [[Image:Sections_same.gif]] | ||
| + | |||
| + | In case an XBRL instance (report) based on this XBRL definition above is reported including values for the corresponding cells in the two tables. <span style="color:#FF3399;font-weight:bold;">The validation will fail since none of the defined combinations is allowed.</span> In the course of dimensional validation the XBRL processor determines the intersection of both sets of combinations within the extended link role and the result will be null. | ||
| + | |||
| + | <br/> | ||
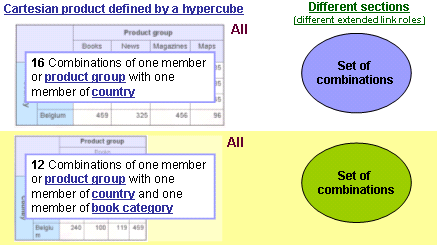
| + | To allow both set of combinations to be reported, the hypercubes have to be defined in different extended link roles. The XBRL processor determines the union of sets of combinations across extended link roles and so <span style="color:#11AABB;font-weight:bold;">the validation will be successful because every combination is allowed</span>. | ||
| + | |||
| + | [[Image:Sections_different.gif]] | ||
| + | |||
| + | ===Application to a sample FINREP table=== | ||
| + | |||
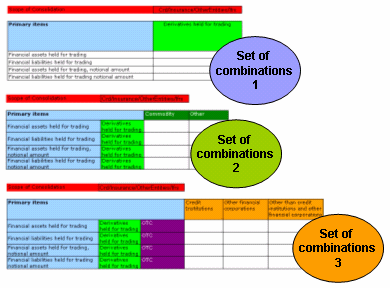
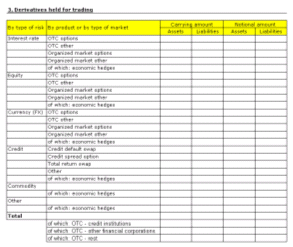
| + | The mapping from a business table to a data structure in XBRL starts with the identification of the measures. They are going to be marked in the specific color. Once the measures are identified an analysis is necessary to find the applicable dimensions. Does each breakdown refer to the same dimension or does it belong to a new category? The result should be documented. In this case it is marked with different colors. | ||
| + | |||
| + | <table width="60%" border="0" cellspacing="0" cellpadding="0"> | ||
| + | <tr> | ||
| + | <td width="45%" valign="top">[[Image:Finrep_table1.gif]] | ||
| + | </td> | ||
| + | <td width="10%"> | ||
| + | </td> | ||
| + | <td width="45%" valign="top">[[Image:Finrep_table2.gif]] | ||
| + | </td> | ||
| + | </tr> | ||
| + | </table> | ||
| + | |||
| + | After the identification of the measures and dimensions the sections have to be identified. As described above all of them consists of a set of combinations with different numbers of dimensions. A normalised view of the tables could be presented as shown in the picture below. Combinations represented in the tables as cells that are not allowed to be reported could be marked in gray. | ||
| + | |||
| + | [[Image:Sections_finrep.gif]] | ||
| = [http://groups.google.com/group/eurofiling/web/readme_matrix_schema.pdf Matrix Schema readme] = | = [http://groups.google.com/group/eurofiling/web/readme_matrix_schema.pdf Matrix Schema readme] = | ||
Current revision

Contribution dated 2009-11-03
ALL TOPICS ARE STILL ON DISCUSSION!
Contents |
Abstract
This document should help users of the CEBS taxonomie (COREP and FINREP) to understand the Matrix Schemas published on www.eurfiling.info web site. In the following the basic aspects of the mulitdimensional data models are explained.
Multidimensional terminology
Description
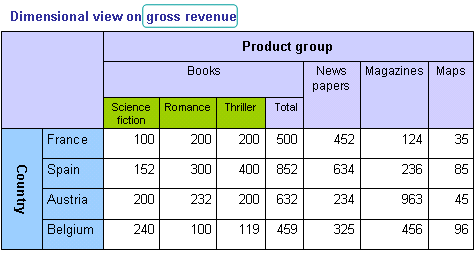
Most of the data presented in tables can be divided in different categories or rather breakdowns. In the table below the gross revenue is broken down by product group and country. The information contained is far more detailed as showing only the aggregated sum of gross revenue and allows therefore a more comprehensive analysis. Multidimensionality is widely used for cost accounting and the corresponding supervision.
The table shows a two dimensional view on the data but in fact three dimensions are included.
Measures
The data that is analysed often in aggregations are called maeasures because they are (mostly) numeric values and measureable. Having only gross revenue and a value is not enough to interpret the data so they are analysed by using "by" conditions. Those "by" conditions are reflected in the example above "by" product group and "by" country.
Multidimensional data is often shown as three dimensional cube. The restriction on three dimensions is based on the limitations of the graphical representation.
A cell in the cube corresponds to a cell in the table.
Dimensions
"By" conditions are called dimensions. Dimensions are views for which data should be stored and they can vary depending on the underlying framework. Some dimensions can be seen as general like time or measure unit.
In the example above the country represents a list of possible countries but other dimensions also representing countries could be "country of origin" or "buying country".
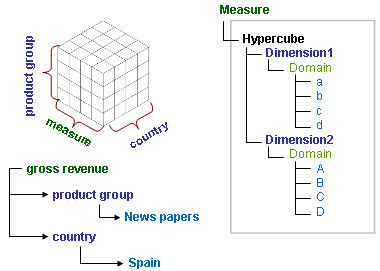
Domain
A domain is a set of items having a specific coherence. This domain can be assigned to a dimension. A sub domain is a subset of items of a domain. A sub domain can also be assigned to a dimension, ie. European countries.
In the CEBS framework domains consists of all possible breakdown items like exposure classes or counterparties. If one table does not include all the possible items and using only a shortened list, a sub domain is created.
Domain member
One item in the data set representing a domain is called domain member. In a CEBS taxonomy they are built up in a domain-member-ship.
Each combination of a measure with the according dimension - domain member combinations identifies a data set uniquely.
Hypercube
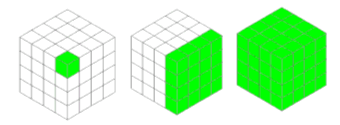
A hypercube defines the cartesian product of the combinations of measures and dimensions. Hypercubes can be assigned to measures. A grahical representation of a hypercube in an XBRL taxonomy is shown below. The dimension members are attached to a domain. The domains are attached to a dimension and the dimensions are assigned to a hypercube.
Depending on the position of the measure in the hierarchy (domain-member-ship) a hypercube can be defined for cells, group of cells or a complete cube (table).
Section
In this case the example table has been extended by an additional breakdown of book category.
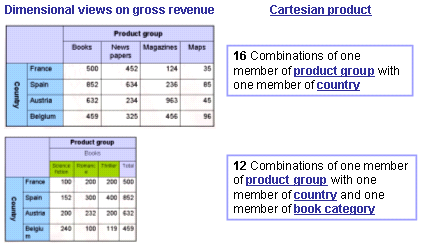
The table can be devided in different parts which are characterised by different number of breakdowns. Both tables refer to the same measure but the first one consists of two dimensions and the second one of three. A Cartesian product is the product of two sets, so the product set contains all possible combinations of one element from each set. The idea can be extended to products of any number of sets. The product set based on two finite sets can be represented by a table. Each cell of this table is a combination of one element of the set row and one element of the set column.
In the example above the Cartesian product of section one consists of 16 Combinations of one member of product group with one member of country. Section two contains 12 Combinations of one member of product group with one member of country and one member of book category.
In XBRL Cartesian products are represented by hypercubes defined in extended link roles within the definition linkbase. Hypercubes that contain combinations that are allowed to be reported, are defined as all hypercubes. With reference to the example above both hypercubes represent allowed combinations. In the picture below both hypercubes are defined in the same extended link role.
In case an XBRL instance (report) based on this XBRL definition above is reported including values for the corresponding cells in the two tables. The validation will fail since none of the defined combinations is allowed. In the course of dimensional validation the XBRL processor determines the intersection of both sets of combinations within the extended link role and the result will be null.
To allow both set of combinations to be reported, the hypercubes have to be defined in different extended link roles. The XBRL processor determines the union of sets of combinations across extended link roles and so the validation will be successful because every combination is allowed.
Application to a sample FINREP table
The mapping from a business table to a data structure in XBRL starts with the identification of the measures. They are going to be marked in the specific color. Once the measures are identified an analysis is necessary to find the applicable dimensions. Does each breakdown refer to the same dimension or does it belong to a new category? The result should be documented. In this case it is marked with different colors.
|
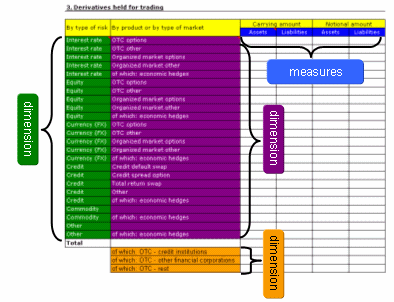
|
After the identification of the measures and dimensions the sections have to be identified. As described above all of them consists of a set of combinations with different numbers of dimensions. A normalised view of the tables could be presented as shown in the picture below. Combinations represented in the tables as cells that are not allowed to be reported could be marked in gray.
Matrix Schema readme
FINREP Matrix Schema 2.0
This is the working area for Data Model and Matrix Schemas. The original documents are stored at Eurofiling Google Group